funçao por : Phelipe Silva

https://youtu.be/rPYCsZpT6ro

Função Afim 2

https://www.youtube.com/watch?v=WuK1V30imuY&feature=youtu.be

Função Afim

https://www.youtube.com/watch?v=reYXc8VuWnk

Função Quadrática

https://www.youtube.com/watch?v=JnGgbQo8za8

Função do 1º grau

Função do 1º grau

A formação de uma função do 1º grau é expressa da seguinte forma: y = ax + b, onde a e b são números reais e a é diferente de 0.

Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.

 Veja alguns exemplos de funções polinomiais do 1º grau:

 f(x) = 5x - 3, onde a = 5 e b = - 3
 f(x) = -2x - 7, onde a = -2 e b = - 7
 f(x) = 11x, onde a = 11 e b = 0

Consideremos x e y duas variáveis, sendo uma dependente da outra, isto é, para cada valor atribuído a x corresponde um valor para y. Definimos essa dependência como função, nesse caso, y está em função de x. O conjunto de valores conferidos a x deve ser chamado de domínio da função e os valores de y são a imagem da função.Esse tipo de função deve ser dos Reais para os Reais.

A representação gráfica de uma função do 1º grau é uma reta. Analisando a lei de formação y = ax + b, notamos a dependência entre x e y, e identificamos dois números: a e b. Eles são os coeficientes da função, o valor de a indica se a função é crescente ou decrescente e o valor de b indica o ponto de intersecção da função com o eixo y no plano cartesiano. Observe:

Função crescente                                                            Função decrescente 




Função crescente: à medida que os valores de x aumentam, os valores correspondentes em y também aumentam.

Função decrescente: à medida que os valores de x aumentam, os valores correspondentes de y diminuem. 

Exemplos de funções do 1º grau

y = 4x + 2, a = 4 e b = 2

y = 5x – 9, a = 5 e b = –9

y = – 2x + 10, a = – 2 e b = 10

y = 3x, a = 3 e b = 0

y = – 6x – 1, a = – 6 e b = – 1 

y = – 7x + 7, a = –7 e b = 7

Raiz ou zero de uma função do 1º grau 

Para determinar a raiz ou o zero de uma função do 1º grau é preciso considerar
y = 0. De acordo com gráfico, no instante em que y assume valor igual a zero, a reta intersecta o eixo x em um determinado ponto, determinando a raiz ou o zero da função.

Vamos determinar a raiz das funções a seguir:

y = 4x + 2 
y = 0
4x + 2 = 0
4x = –2
x = –2/4
x = –1/2
A reta representada pela função y = 4x + 2 intersecta o eixo x no seguinte valor: –1/2


y = – 2x + 10
y = 0
– 2x + 10 = 0
– 2x = – 10 (–1)
2x = 10
x = 10/2
x = 5
A reta representada pela função y = – 2x + 10 intersecta o eixo x no seguinte valor: 5 

y = – 7x + 7
y = 0
–7x + 7 = 0
–7x = –7
x = 1
A reta representada pela função y = –7x + 7 intersecta o eixo x no seguinte valor: 1

y = 3x
y = 0
3x = 0
x = 0
A reta representada pela função y = 3x intersecta o eixo x no seguinte valor: 0

Coordenadas do Vértice de uma Parábola

Para determinarmos os vértices de uma parábola temos que encontrar o par ordenado de pontos que constituem as coordenadas de retorno da parábola. Esse ponto de retorno da parábola, mais conhecido como vértice da parábola, pode ser calculado com base nas expressões matemáticas envolvendo os coeficientes da função do 2º grau dada pela lei de formação y = ax² + bx + c. 

O valor de x na determinação do vértice de uma parábola é dado por  e o valor de y é calculado por  . Nesse caso, temos que, quando o coeficiente a for maior que zero, a parábola possui valor mínimo e quando a menor que zero, valor máximo. 


Valor mínimo (a > 0)

Valor máximo (a < 0) 

Exemplo 
Para produzirmos x unidades de uma mercadoria, temos que o custo dessa produção em reais é dado pela expressão matemática C = x² – 80x + 3000. Com base nessa expressão, determine a quantidade de unidades produzidas para que o custo seja mínimo e qual o valor mínimo do custo. 

Quantidade de unidades produzidas para que o custo seja mínimo será de 40 peças. Observe:

Valor mínimo do custo será de R$ 1 400,00. Veja:

logaritimos por Phelipe silva

https://youtu.be/ygZsXGAr6Xg

Função Quadrática

 Função Quadrática

  Definição
    Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax² + bx + c, onde a, b e c são números reais e a 0.
    Vejamos alguns exemplos de função quadráticas:

1. f(x) = 3x² - 4x  + 1, onde a = 3, b = - 4 e c = 1
2. f(x) = x² -1, onde a = 1, b = 0 e c = -1
3. f(x) = 2x² + 3x + 5, onde a = 2, b = 3 e c = 5
4. f(x) = - x² + 8x, onde a = -1, b = 8 e c = 0
5. f(x) = -4x², onde a = - 4, b = 0 e c = 0

Gráfico
    O gráfico de uma função polinomial do 2º grau, y = ax² + bx + c, com a 0, é uma curva chamada parábola.
Exemplo:
    Vamos construir o gráfico da função y = x² + x:
    Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.

x y -3 6 -2 2 -1 0 0 0 1 2 2 6

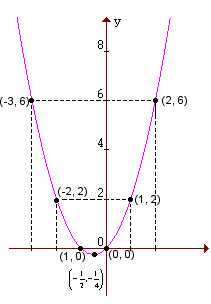    Observação:

   Ao construir o gráfico de uma função quadrática y = ax² + bx + c, notaremos sempre que:

• se   a > 0, a parábola tem a concavidade voltada para cima;
• se   a < 0, a parábola tem a concavidade voltada para baixo;

Zero e Equação do 2º Grau

    Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax² + bx + c , a 0, os números reais x tais que f(x) = 0.

    Então as raízes da função f(x) = ax² + bx + c são as soluções da equação do 2º grau ax² + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:

    Temos:

                   

Observação

   A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando 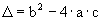,  chamado discriminante, a saber:

• quando é positivo, há duas raízes reais e distintas;
• quando é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);
• quando é negativo, não há raiz real.