Função Quadrática
DefiniçãoChama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a
Vejamos alguns exemplos de função quadráticas:
- f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
- f(x) = x2 -1, onde a = 1, b = 0 e c = -1
- f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
- f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
- f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a
Exemplo:
Vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
| 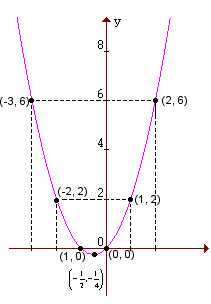 |
Observação:
Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
- se a > 0, a parábola tem a concavidade voltada para cima;
- se a < 0, a parábola tem a concavidade voltada para baixo;
Zero e Equação do 2º Grau
Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a  0, os números reais x tais que f(x) = 0.
0, os números reais x tais que f(x) = 0.
Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:
Temos:
Observação
A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando 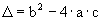 , chamado discriminante, a saber:
, chamado discriminante, a saber:
- quando
 é positivo, há duas raízes reais e distintas;
é positivo, há duas raízes reais e distintas; - quando
 é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);
é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais); - quando
 é negativo, não há raiz real.
é negativo, não há raiz real.
Nenhum comentário:
Postar um comentário